Algunos de los métodos que hemos usado, como los métodos matemáticos, devuelven valores. Pero todos los métodos que hemos escrito en el capítulo anterior han sido nulos (void); es decir, no producen valores de retorno. En este capítulo, escribiremos métodos que devuelven valores, llamados value methods.
Cuando invocamos a un método nulo, la invocación generalmente se realiza en una sola línea.
Por ejemplo, aquí está hay método de conteo (countup).
1
2
3
4
5
6
7
8
public static void countup(int n) {
if (n == 0) {
System.out.println("Blastoff!");
} else {
countup(n - 1);
System.out.println(n);
}
}
Y aquí esta cómo se invoca:
1
2
countup(3);
System.out.println("Have a nice day.");
Por otro lado, cuando invocamos un value method, tenemos que hacer algo con el valor de retorno. Por lo general, lo asignamos a una variable o lo usamos como parte de una expresión, como esta:
1
2
double error = Math.abs(expected - actual);
double height = radius * Math.sin(angle);
En comparación con los métodos void, los métodos de valor difieren de dos maneras:
- Declaran el tipo del valor de retorno (el tipo devuelto);
- Usan al menos una declaración de devolución para proporcionar un valor de retorno.
Aquí hay un ejemplo: calculateArea toma un double como parámetro y devuelve el área del círculo con ese radio:
1
2
3
4
public static double calculateArea(double radius) {
double result = Math.PI * radius * radius;
return result;
}
Como de costumbre, este método es público y estático. Pero en el lugar donde estamos acostumbrados a ver void, vemos double, lo que significa que el valor de retorno de este método es un double. La última línea es una nueva forma de declaración de devolución que incluye un valor de retorno. Esta declaración significa, “regrese inmediatamente de este método y use la siguiente expresión como el valor de retorno”. La expresión que se proporcione puede ser arbitrariamente compleja, por lo que podríamos haber escrito este método de manera más concisa:
1
2
3
public static double calculateArea(double radius) {
return Math.PI * radius * radius;
}
Por otro lado, las variables temporales como resultado a menudo hacen que la depuración sea más fácil, especialmente cuando estamos pasando por el código usando un depurador
El tipo de expresión en la declaración de devolución debe coincidir con el tipo de retorno del método. Cuando declara que el tipo de devolución es double, estamos haciendo la promesa de que este método producirá un valor double. Si intenta regresar sin expresión, o una expresión con el tipo incorrecto, el compilador generará un error.
A veces es útil tener múltiples declaraciones de devolución, por ejemplo, una en cada rama de un condicional:
1
2
3
4
5
6
7
public static double absoluteValue(double x) {
if (x < 0) {
return -x;
} else {
return x;
}
}
Dado que estas declaraciones de retorno están en una declaración condicional, solo una será ejecutada. Tan pronto como cualquiera de ellas se ejecuta, el método termina sin ejecutar más declaraciones. El código que aparece después de una declaración de devolución (en el mismo bloque) o en cualquier lugar donde nunca se pueda ejecutar, se llama código muerto (dead code_). El compilador dará un error de “unreachable statement” si parte de nuestro código está muerto. Por ejemplo, este método contiene un código muerto:
1
2
3
4
5
6
7
8
public static double absoluteValue(double x) {
if (x < 0) {
return -x;
} else {
return x;
}
System.out.println("This line is dead.");
}
Si colocamos declaraciones de devolución dentro de una declaración condicional, tenemos que asegurarnos de que cada ruta posible a través del programa llegue a una declaración de retorno. El compilador nos informará si este no es el caso. Por ejemplo, el siguiente método está incompleto:
1
2
3
4
5
6
7
8
public static double absoluteValue(double x) {
if (x < 0) {
return -x;
} else if (x > 0) {
return x;
}
// syntax error
}
Cuando x es 0, ninguna condición es verdadera, por lo que el método finaliza sin alcanzar una declaración de devolución. El mensaje de error en este caso podría ser algo así como “missing return statement”, que es confusa ya que hay dos returns. Pero con suerte sabrás lo que significa.
1 Escribir métodos
Los principiantes a menudo cometen el error de escribir un montón de código antes de intentar compilar y ejecutarlo. Luego pasan demasiado tiempo depurando. Un mejor enfoque es lo que llamamos desarrollo incremental. Los aspectos clave de desarrollo incremental son:
- Comenzar con un programa que funcione y realizar pequeños cambios incrementales. En cualquier momento, si hay un error, sabremos dónde buscar.
- Usar variables para mantener los valores intermedios para poder verificarlos, ya sea con instrucciones de impresión o mediante el uso de un depurador.
- Una vez que el programa está funcionando, podemos consolidar varias declaraciones en expresiones compuestas (pero solo si no hace que el programa sea más difícil de leer).
Como ejemplo, supongamos que queremos encontrar la distancia entre dos puntos, dado por las coordenadas (x1, y1) y (x2, y2). Por la definición habitual:

El primer paso es considerar cómo debería ser un método para calcular la distancia en Java.
En otras palabras, ¿cuáles son las entradas (parámetros) y cuál es la salida? (valor de retorno)? En este caso, los dos puntos son los parámetros, y es natural para representarlos usando cuatro valores double. El valor de retorno es el distancia, que también debería tener tipo double.
Ya podemos escribir un esquema para el método, que a veces se llama stub. El stub incluye la signatura del método y una declaración de devolución:
1
2
3
public static double distance(double x1, double y1, double x2, double y2) {
return 0.0;
}
La declaración de devolución es un marcador de posición que es necesario para que el programa pueda compilar. En esta etapa, el programa no hace nada útil, pero es bueno compilarlo para que podamos encontrar cualquier error de sintaxis antes de agregar más código. Por lo general, es una buena idea pensar en las pruebas antes de desarrollar nuevos métodos; hacerlo puede ayudarlo a descubrir cómo implementarlos. Para probar el método, podemos invocarlo desde main usando valores de muestra:
1
double dist = distance(1.0, 2.0, 4.0, 6.0);
Con estos valores, la distancia horizontal es 3.0 y la distancia vertical es 4.0. Entonces el resultado debería ser 5.0, la hipotenusa de un triángulo 3-4-5. Cuando estamos probando un método, es útil saber la respuesta correcta.
Una vez que hemos compilado el código auxiliar, podemos comenzar a agregar líneas de código una a una. Después de cada cambio incremental, volvemos a compilar y ejecutar el programa. Si hay un error en cualquier punto, tenemos una buena idea de dónde buscar: la última línea que agregamos.
El siguiente paso es encontrar las diferencias x2 - x1 y y2 - y1. Almacenamos esos valores en variables temporales llamadas dx y dy.
1
2
3
4
5
6
7
public static double distance (double x1, double y1, double x2, double y2) {
double dx = x2 - x1;
double dy = y2 - y1;
System.out.println("dx is " + dx);
System.out.println("dy is " + dy);
return 0.0;
}
Las instrucciones de impresión nos permiten verificar los valores intermedios antes de proceder Deberían ser 3.0 y 4.0. Eliminaremos las declaraciones impresas cuando el método está terminado. El código como ese se llama scaffolding, porque es útil para construir el programa, pero no es parte del producto final.
El siguiente paso es hacer el cuadrado de dx y dy. Podríamos usar el método Math.pow, pero es más simple multiplicar cada término por sí mismo.
1
2
3
4
5
6
7
public static double distance (double x1, double y1, double x2, double y2) {
double dx = x2 - x1;
double dy = y2 - y1;
double dsquared = dx * dx + dy * dy;
System.out.println("dsquared is " + dsquared);
return 0.0;
}
De nuevo, debemos compilar y ejecutar el programa en esta etapa y verificar el valor intermedio, que debería ser 25.0. Finalmente, podemos usar Math.sqrt para calcular y devolver el resultado.
1
2
3
4
5
6
7
public static double distance (double x1, double y1, double x2, double y2) {
double dx = x2 - x1;
double dy = y2 - y1;
double dsquared = dx * dx + dy * dy;
double result = Math.sqrt(dsquared);
return result;
}
A medida que ganemos más experiencia en programación, podremos escribir y depurar más de una línea a la vez. Sin embargo, el desarrollo incremental puede salvarnos un montón de tiempo.
2 Composición de métodos
Una vez que definimos un nuevo método, podemos usarlo como parte de una expresión, o construir nuevos métodos usando métodos existentes. Por ejemplo, supongamos que alguien nos da dos puntos, el centro del círculo y un punto en el perímetro, y pregunta por el área del círculo. Digamos que el punto central se almacena en las variables xc y yc, y el punto del perímetro está en xp y yp.
El primer paso es encontrar el radio del círculo, que es la distancia entre los dos puntos. Afortunadamente, tenemos un método que hace exactamente eso (distance).
1
double radius = distance(xc, yc, xp, yp);
El segundo paso es encontrar el área de un círculo con ese radio. Tenemos un método para ese cálculo también (calculateArea).
1
2
double area = calculateArea(radius);
return area;
Juntándolo todo en un nuevo método, nos queda:
1
2
3
4
5
public static double circleArea(double xc, double yc, double xp, double yp) {
double radius = distance(xc, yc, xp, yp);
double area = calculateArea(radius);
return area;
}
Las variables temporales radius y area son útiles para el desarrollo y depuración, pero una vez que el programa está funcionando podemos hacerlo más conciso componiendo las llamadas a los métodos:
1
2
3
public static double circleArea (double xc, double yc, double xp, double yp) {
return calculateArea(distance(xc, yc, xp, yp));
}
Este ejemplo demuestra un proceso llamado descomposición funcional; esto es, dividir un cálculo complejo en métodos simples, probando los métodos de forma aislada, y luego componer los métodos para realizar el cálculo.
Este proceso reduce el tiempo de depuración y produce un código que es más probable que sea correcto y más fácil de mantener.
3 Sobrecarga (overloading)
Podéis haber notado que circleArea y calculateArea realizan funciones similares. Ambos encuentran el área de un círculo, pero toman diferentes parámetros. Para calculateArea, tenemos que proporcionar el radio; para circleArea proporcionar dos puntos. Si dos métodos hacen lo mismo, es natural darles el mismo nombre.
Tener más de un método con el mismo nombre se llama sobrecarga, y es legal en Java siempre que cada versión tome diferentes parámetros. Asi que podríamos cambiar el nombre circleArea por calculateArea:
1
2
3
public static double calculateArea(double xc, double yc, double xp, double yp) {
return calculateArea(distance(xc, yc, xp, yp));
}
Tened en cuenta que este nuevo método de cálculo de área no es recursivo. Cuando invocamos un método sobrecargado, Java sabe qué versión quieres mirando los argumentos que proporcionamos. Si escribimos:
1
double x = calculateArea(3.0);
Java busca un método llamado calculateArea que toma una double como argumento, y entonces usa la primera versión, que interpreta el argumento como radio. Si escribimos:
1
double y = calculateArea(1.0, 2.0, 4.0, 6.0);
Java usa la segunda versión de calculateArea, que interpreta los argumentos como dos puntos. En este ejemplo, la segunda versión en realidad invoca a la primera versión.
Muchos métodos Java están sobrecargados, lo que significa que hay diferentes versiones que aceptan diferentes número o tipo de parámetros. Por ejemplo, hay versiones de print y println que aceptan un solo parámetro de cualquier tipo de dato. En la clase de Math, hay una versión de abs (valor absoluto) que funciona en doubles, y también hay una versión para ints.
Aunque la sobrecarga es una característica útil, debe usarse con precaución. Puede llegar a confundir mucho si estamos intentando depurar una versión de un método mientras invocamos accidentalmente uno diferente.
4 Métodos booleanos
Los métodos pueden devolver valores booleanos, al igual que cualquier otro tipo, que a menudo resulta conveniente para ocultar pruebas dentro de métodos. Por ejemplo:
1
2
3
4
5
6
7
public static boolean isSingleDigit(int x) {
if (x > -10 && x < 10) {
return true;
} else {
return false;
}
}
El nombre de este método es isSingleDigit. Es común dar a los métodos booleanos nombres que suenen como preguntas sí / no. Dado que el tipo de devolución es boolean, la instrucción return debe proporcionar una expresión booleana. El código en sí es sencillo, aunque es más largo de lo que necesita ser.
Recordad que la expresiónx> -10 && x <10 tiene un tipo booleano, por lo que no tiene nada de malo devolverlo directamente (sin la instrucción if):
1
2
3
public static boolean isSingleDigit(int x) {
return x > -10 && x < 10;
}
En main, podemos invocar el método de la forma habitual:
1
2
System.out.println(isSingleDigit(2));
boolean bigFlag = !isSingleDigit(17);
La primera línea muestra true porque 2 es un número de un solo dígito. La segunda línea establece bigFlag también a true , porque 17 no es un número de un solo dígito.
Las instrucciones condicionales a menudo invocan métodos booleanos y usan el resultado como la condición:
1
2
3
4
5
if (isSingleDigit(z)) {
System.out.println("z is small");
} else {
System.out.println("z is big");
}
Ejemplos como este casi se leen en español “Si es un solo dígito z, imprime … sino imprime … “.
5 Métodos recursivos
Vamos a explorar una de las cosas más mágicas que un programa puede hacer: recursión. Considera el siguiente ejemplo:
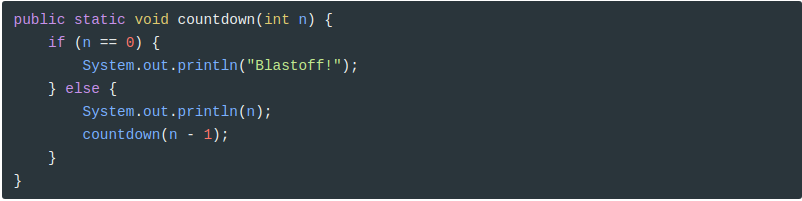
El nombre del método es countdown; toma un solo entero como parámetro. Si el parámetro es cero, muestra la palabra “Blastoff”. De lo contrario, muestra el número y luego se invoca a sí mismo, pasando n - 1 como argumento. Un método que se invoca a sí mismo se llama recursivo.
¿Qué sucede si invocamos countdonw(3) desde main?
1
2
3
4
5
6
7
La ejecución de countdonw comienza con n == 3, y dado que n no es cero, muestra el valor 3, y luego se invoca a sí mismo ...
La ejecución de countdonw comienza con n == 2, y como n no es cero, muestra el valor 2, y luego se invoca a sí mismo ...
La ejecución de countdonw comienza con n == 1, y dado que n no es cero, muestra el valor 1, y luego se invoca a sí mismo ...
La ejecución de countdonw comienza con n == 0, y dado que n es cero, muestra la palabra "Blastoff!" y luego regresa.
countdonw que obtuvo n == 1 regresa.
countdonw que obtuvo n == 2 regresa.
countdonw que obtuvo n== 3 regresa.
Y ahora estamos de vuelva en main. Así que, al final, la salida es:
1
2
3
4
3
2
1
Blastoff!
Como un segundo ejemplo, reescribiremos los métodos newLine y threeLine que vimos en el tema void methods.

Aunque estos métodos funcionan, no ayudarían si quisiéramos mostrar dos nuevas líneas, o tal vez 100. Una mejor alternativa sería:

Este método toma un entero, n, como parámetro y muestra n nuevas líneas. La estructura es similar a la cuenta regresiva (countdown). Siempre que n sea mayor que cero, muestra una nueva línea y luego se invoca a sí mismo para mostrar (n - 1) nuevas líneas adicionales. El número total de nuevas líneas es 1 + (n - 1), que es justo lo que queríamos: n.
En un método recursivo siempre debe haber un caso en que no se produzca la recursión. Este caso es llamado caso base.
En los métodos nLines y countdown, el caso base se produce cuando n es igual a 0. Si un método recursivo no tiene caso base o este nunca llega a alcanzarse, el programa entraría en un bucle infinito, aunque acabará en algún momento dando el error StackOverflowError.
El siguiente programa no tiene caso base:

Este método muestra la cadena hasta que la pila de java se desborda, en ese punto arroja una excepción.
6 Números binarios
El ejemplo countdown tiene tres partes: (1) verifica el caso base, (2) muestra algo, y (3) hace una llamada recursiva. ¿Qué crees que pasa si se revierten los pasos 2 y 3, haciendo la llamada recursiva antes de mostrar el resultado?
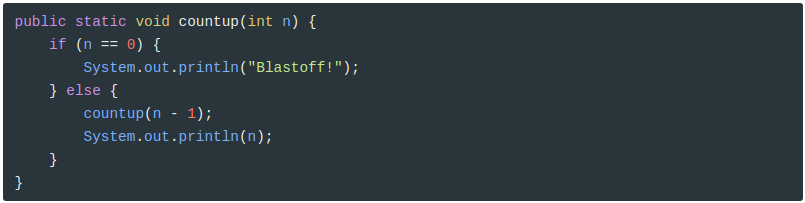
Ahora System.out.println ocurre antes que cada llamada recursiva regrese. Como resultado se obtiene una cuenta hacia adelante en vez de una cuenta atrás:
1
2
3
4
Blastoff!
1
2
3
Este comportamiento es útil cuando es más fácil calcular los resultados en orden inverso. Por ejemplo, para convertir un entero decimal en su representación binaria, se divide repetidamente el número por dos:
1
2
3
4
5
23 / 2 da 11 y resto 1
11 / 2 da 5 y resto 1
5 / 2 da 2 y resto 1
2 / 2 da 1 y resto 0
1 / 2 da 0 y resto 1
Al leer estos restos de abajo hacia arriba, 23 en binario es 10111. Para saber más sobre los números binarios, visita http://www.mathsisfun.com/binary-number-system.html.
Aquí hay un método recursivo que muestra la representación binaria de cualquier entero positivo:
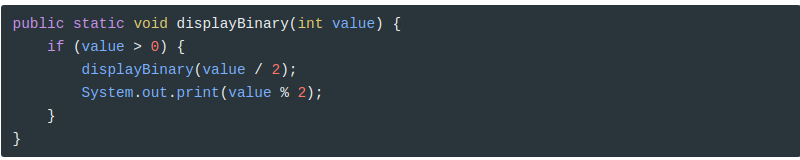
Si el valor es cero, displayBinary no hace nada (ese es el caso base). Si el argumento es positivo, el método lo divide por dos y llama a displayBinary recursivamente. Cuando la llamada recursiva vuelve, el método muestra un dígito del resultado y regresa (nuevamente).
Aprender a pensar recursivamente es un aspecto importante para aprender a pensar como un científico de la computación. Muchos algoritmos se pueden escribir de forma concisa con métodos recursivos que realizan cálculos en el camino hacia abajo, en el camino ascendente o ambos.
7 Más recursión
Muchas funciones matemáticas se definen recursivamente, porque a menudo esa es la forma más simple. Por ejemplo, el factorial de un entero n, que está escrito n!, se define así:

¡No confundir el símbolo matemático !, que significa factorial, con el operador de Java !, que significa negación. Esta definición dice que factorial(0) es 1, y que factorial(n) es n x factorial (n - 1).
Así que factorial(3) es 3 x factorial(2); factorial(2) es 2 x factorial(1); factorial(1) es 1 x factorial(0); y factorial(0) es 1. Poniéndolo todo junto tenemos, 3 x 2 x 1 x 1, que es 6.
Si se puede formular una definición recursiva de algo, se puede escribir fácilmente un método de Java para evaluarlo. El primer paso es decidir qué parámetros y el tipo de devolución del método. Dado que factorial se define para enteros, el método requiere un int como parámetro y devuelve un int. Así que aquí hay un buen lugar para comenzar:
1
2
3
public static int factorial(int n) {
return 0;
}
Luego, pensamos en el caso base. Si el argumento pasa a ser 0, se devuelve 1.
1
2
3
4
5
6
public static int factorial(int n) {
if (n == 0) {
return 1;
}
return 0;
}
De lo contrario, y esta es la parte interesante, tenemos que hacer una llamada recursiva para encontrar el factorial de n - 1, y luego multiplicarlo por n.
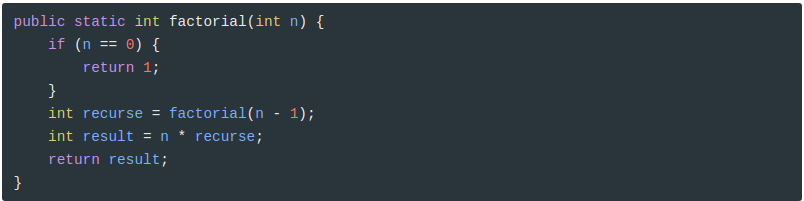
El flujo de ejecución de este programa es similar a countdown. Si invocamos factorial con el valor 3:
1
2
3
4
5
6
7
Como 3 no es cero, tomamos la segunda rama y calculamos factorial de n - 1 ...
Como 2 no es cero, tomamos la segunda rama y calculamos el factorial de n - 1 ...
Como 1 no es cero, tomamos la segunda rama y calculamos el factorial de n - 1 ...
Como 0 es cero, tomamos la primera rama y devuelve el valor 1 inmediatamente.
El valor de retorno (1) se multiplica por n, que es 1, y el resultado es devuelto.
El valor de retorno (1) se multiplica por n, que es 2, y el resultado es devuelto
El valor de retorno (2) se multiplica por n, que es 3, y el resultado, 6, se devuelve (3) a quien haya invocado a factorial.
La figura siguiente muestra cómo se ve el diagrama de pila para esta secuencia de invocaciones del método. Los valores de retorno se muestran volviendo a pasar por la pila. Observad que recurse y result no existen en el último cuadro, porque cuando n == 0 el código que los declara no se ejecuta.

8 Salto de fe (leap of faith)
Seguir el flujo de ejecución es una forma de leer programas, pero se puede convertir en abrumador rápidamente. Una alternativa es el salto de fe: cuando llegamos a una invocación de un método, en lugar de seguir el flujo de ejecución, asumimos que el método funciona correctamente y que devuelve el valor apropiado.
De hecho, ya estamos practicando un acto de fe cuando usamos métodos de la Biblioteca de Java, como cuando invocamos Math.cos o System.out.println, no examinamos las implementaciones de esos métodos. Solo asumimos que funcionan correctamente.
Debemos aplicar el mismo razonamiento a nuestros propios métodos. Por ejemplo, escribimos un método llamado isSingleDigit que determina si un número está entre 0 y 9. Una vez que nos convencemos de que este método es correcto - al probar y examinar el código - podemos usar el método sin siquiera mirar la implementación de nuevo.
Lo mismo es cierto para los métodos recursivos. Cuando llegamos a la llamada recursiva, en lugar de seguir el flujo de ejecución, debemos suponer que la invocación al método recursivo funciona. Por ejemplo, “Asumiendo que puedo encontrar el factorial de n - 1, ¿podemos calcular el factorial de n? “Sí se puede, multiplicando por n. Por supuesto, es extraño suponer que el método funciona correctamente cuando no hemos terminado de escribirlo, ¡pero es por eso que se llama un acto de fe!
9 Otro ejemplo
Otra función matemática común definida recursivamente es la secuencia de Fibonacci, que tiene la siguiente definición:

Traducido a Java, el método es

Si intentas seguir el flujo de ejecución aquí, incluso para valores pequeños de n, nuestra cabeza explotará. Pero si damos un salto de fe y suponemos que las dos invocaciones recursivas funcionan correctamente, está claro que su suma es el resultado.
Vocabulario
- tipo de retorno: el tipo de valor que devuelve un método.
- valor de retorno: el valor proporcionado como resultado de una invocación a un método.
- variable temporal: una variable de corta duración, a menudo utilizada para la depuración.
- código muerto: parte de un programa que nunca se puede ejecutar, a menudo porque aparece después de una declaración de devolución.
- desarrollo incremental: un proceso para crear programas escribiendo algunas líneas a la vez, compilando y probando.
- stub: marcador de posición para un método incompleto para que la clase compile.
- scaffolding: Código que se usa durante el desarrollo del programa, pero que no forma parte de la versión final.
- descomposición funcional: Un proceso para descomponer un cálculo complejo en métodos simples, para despúes componer los métodos para realizar el cálculo.
- sobrecarga: definir más de un método con el mismo nombre pero con diferentes parámetros.
- salto de fe: una forma de leer programas recursivos al asumir que la llamada recursiva funciona, en lugar de seguir el flujo de ejecución.
Ejercicios
1 EsDivisible.java Escribe un método llamado esDivisible que toma dos enteros, n y m, y devuelve verdadero si n es divisible por m, y falso en caso contrario.
2 EsTriangulo.java Si te dan tres palitos, puedes o no ser capaz de organizarlos en un triángulo. Por ejemplo, si uno de los palos mide 12 cm de largo y los otros dos tienen un cm de largo, no podrás hacer que los palitos cortos se encuentren en el medio. Para tres longitudes, hay una prueba simple para ver si es posible formar un triángulo:
Si cualquiera de las tres longitudes es mayor que la suma de las otras dos, no puedes formar un triángulo Escribe un método llamado esTriangulo que toma tres enteros como argumentos y devuelve true o false, dependiendo de si puede o no formar un triángulo a partir de palitos con las longitudes dadas.
3 Potencia.java Escribe un método recursivo llamado potencia que toma un doble x y un entero n y devuelve x^n.
Sugerencia: Una definición recursiva de esta operación es

4 Positivos.java Escribe un método llamado positivos que muestre cuántos números de un array son positivos.
5 LetraDni.java Realiza un método llamado letraDni que devuelva la letra correspondiente a un DNI sin letra
6 Primo.java Crea un método llamado esPrimo que devuelva un booleano para indicar si el número pasado como parámetro es primo.
7 Primos.java Crea un programa que muestre en pantalla todos los números primos entre 3 y 100, usando la función creada en el ejercicio anterior. Puedes llamar a la función creada en el ejercicio anterior de la siguiente forma: Primo.esPrimo(numero);
Adaptado del siguiente material