Ejercicios de ampliación

Índice

Lucky number

Se desea conocer el lucky number (número de la suerte) de cualquier persona. Dicho número se consigue reduciendo la fecha de nacimiento a un número de solo un dígito.

Por ejemplo, la fecha de nacimiento de Isabel es:

1

03-09-1971 -> 3 + 9 + 1971 -> 3 + 9 + 1 + 9 + 7 + 1 = 30 -> 3 + 0 = 3

El número de la suerte de Isabel será el 3.

Número Armstrong o narcisista

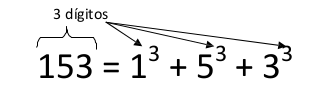
Realiza un método que, dado un número de tres cifras, averigüe si es un número Armstrong. Un número es Armstrong cuando la suma de cada uno de sus dígitos elevado al número de dígitos que componen el número da como resultado el propio número. Veamos un ejemplo:

image-20220927195348667

1
2
3
4

assertEquals(amstrong.armstrong(370), true);
assertEquals(amstrong.armstrong(371), true);
assertEquals(amstrong.armstrong(407), true);
assertEquals(amstrong.armstrong(698), false);

Radares de tramo

La Dirección Particular de Tráfico (DPT) está empeñada en hacer que los conductores respeten los límites de velocidad. Sin entrar en si es por razones de seguridad, por ahorrar combustible, o con un mero afán recaudatorio, ahora sabemos que además de los radares fijos tradicionales, están poniendo en funcionamiento los radares de tramo.

Desde un punto de vista formal, estos radares se basan en el teorema de Lagrange (también llamado de valor medio o de Bonnet-Lagrange), que dice que si tienes una función continua en un intervalo cerrado y derivable en el intervalo abierto, entonces algún punto de ese intervalo abierto tendrá derivada instantánea igual a la pendiente media de la curva en el intervalo cerrado.

Aunque asuste a primera vista, la repercusión es sencilla: si hacemos un viaje desde Madrid a Zaragoza y nuestra velocidad media es de 111Km/h, forzosamente en algún punto del camino, nuestra velocidad ha sido de 111Km/h.

Los radares de tramo consisten en colocar dos cámaras en dos puntos alejados de una carretera para poder comprobar cuánto tiempo ha tardado el coche en recorrer ese tramo. Si la velocidad media supera la velocidad máxima permitida, gracias al teorema anterior podremos saber (aunque no le hayamos visto) que en algún punto del trayecto ha superado esa velocidad. Por ejemplo, si colocamos las cámaras separadas 10Km en un tramo cuya velocidad está limitada a 110Km/h, y un coche tarda 5 minutos en ser visto por la segunda cámara, sabremos que su velocidad media ha sido de 120Km/h, y por tanto en algún sitio ha superado el límite de velocidad aunque al pasar por debajo de las dos cámaras el coche fuera a 80Km/h.

El programa recibe tres datos:

  • distancia en metros que separan los radares
  • velocidad máxima
  • tiempo empleado
1
2
3
4

assertEquals(radar.esMulta(9165, 110, 300), false);
assertEquals(radar.esMulta(9165, 110, 299), true);
assertEquals(radar.esMulta(12000, 100, 433), false);
assertEquals(radar.esMulta(12000, 100, 431), true);

Créditos

Autores: Marco Antonio Gómez Martín, Patricia Díaz García y Pedro Pablo Gómez Martín. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=112

Kaprekar

El matemático indio Dattaraya Ramchandra Kaprekar descubrió en 1949 una curiosa característica del número 6174. Hoy, se conoce a dicho número como constante de Kaprekar en honor a él.

El número es notable por la siguiente propiedad:

  1. Elige un número de cuatro dígitos que tenga al menos dos diferentes (es válido colocar el dígito 0 al principio, por lo que el número 0009 es válido).
  2. Coloca sus dígitos en orden ascendente y en orden descendente para formar dos nuevos números. Puedes añadir los dígitos 0 que necesites al principio.
  3. Resta el menor al mayor.
  4. Vuelve al paso 2.

​ A este proceso se le conoce como la rutina de Kaprekar, y siempre llegará al número 6174 en, como mucho, 7 iteraciones. Una vez en él, el proceso no avanzará, dado que 7641 − 1467 = 6174.

​ Por ejemplo, el número 3524 alcanzará la constante de Kaprekar en 3 iteraciones:

1
2
3

5432 − 2345 = 3087
8730 − 0378 = 8352
8532 − 2358 = 6174

Los únicos dígitos de cuatro cifras para los que la rutina de Kaprekar no alcanza el número 6174 son los repdigits, es decir aquellos cuyas cuatro cifras son iguales (como 1111), pues en la primera iteración se alcanzará el valor 0 y no podrá salirse de él. Es por esto que en el paso 1 se pedía explícitamente que el número inicial tuviera al menos dos dígitos diferentes.

El resto de los números de cuatro cifras terminarán siempre en el número 6174.

A continuación se muestran dos ejemplos más:

  • El número 1121 necesita 5 iteraciones:

​ 2111 − 1112 = 0999
​ 9990 − 0999 = 8991
​ 9981 − 1899 = 8082
​ 8820 − 0288 = 8532
​ 8532 − 2358 = 6174

  • El número 1893 necesita 7:

​ 9831 − 1389 = 8442
​ 8442 − 2448 = 5994
​ 9954 − 4599 = 5355
​ 5553 − 3555 = 1998
​ 9981 − 1899 = 8082
​ 8820 − 0288 = 8532
​ 8532 − 2358 = 6174

1
2
3
4
5

assertEquals(kaprekar.iterations(3524), 3);
assertEquals(kaprekar.iterations(1111), 8);
assertEquals(kaprekar.iterations(1121), 5);
assertEquals(kaprekar.iterations(3524), 3);
assertEquals(kaprekar.iterations(1893), 7);

Créditos

Autores: Pedro Pablo Gómez Martín, Patricia Díaz García y Marco Antonio Gómez Martín.

Fuente: https://www.aceptaelreto.com/problem/statement.php?id=100

Códigos de barras

En el lejano 1952, tres norteamericanos patentaron lo que terminó llamándose código de barras. Consiste en una técnica para representar números (y, en menos ocasiones, letras) mediante una serie de líneas verticales paralelas, con diferentes grosores y separaciones entre ellas. Si bien el primer uso sirvió para identificar de manera automática los vagones de un ferrocarril, hoy los códigos de barras se utilizan en infinidad de lugares, siendo la catalogación de productos la más habitual.

La manera concreta de codificar mediante barras los números y las letras puede ser muy variada, lo que ha llevado a la aparición de diferentes estándares. De todos ellos, el EAN (European Article Number) resulta ser el más extendido. De éste, hay principalmente dos formatos, que se diferencian en el ancho. Existe así el llamado EAN-8, que codifica 8 números, y el EAN-13, que, naturalmente, codifica 13.

image-20221006172603328

El último dígito del código se utiliza para detección de errores, y se calcula a partir de los demás. Para eso:

  • Empezando por la derecha (sin contar el dígito de control que se está calculando), se suman los dígitos individuales, multiplicados por un factor:

    • Los dígitos en posiciones impares (empezando a contar por la derecha saltándonos el de control) se multiplican por 3.
    • Los dígitos en posiciones pares se multiplican por 1.

    Por ejemplo, para el código EAN-8 de la figura la operación a realizar es:

    2 · 3 + 5 · 1 + 9 · 3 + 3 · 1 + 8 · 3 + 5 · 1 + 6 · 3 = 88

  • El dígito de comprobación es el número que hay que sumar al resultado anterior para llegar a un valor múltiplo de 10. En el ejemplo de EAN-8, para llegar al múltiplo de 10 más cercano por encima del número 88 hay que sumar 2 (y llegar al 90). Ten en cuenta que si la suma resulta ser ya múltiplo de 10, el dígito de control será 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import org.junit.Test;

import static org.junit.Assert.*;

public class CodigoBarrasTest {

    @Test
    public void check() {
        assertEquals(true, CodigoBarras.check("65839526"));
        assertEquals(false, CodigoBarras.check("65839521"));
        assertEquals(true, CodigoBarras.check("8414533043847"));
        assertEquals(true, CodigoBarras.check("5029365779425"));
        assertEquals(false, CodigoBarras.check("5129365779425"));

    }
}

Créditos

Autores: Pedro Pablo Gómez Martín, Marco Antonio Gómez Martín y Patricia Díaz García.

Fuente: https://www.aceptaelreto.com/problem/statement.php?id=106

Escudos del ejército romano

Son famosas las formaciones que el antiguo ejército romano utilizaba para entrar en batalla. En esas formaciones, los legionarios se agrupaban en una figura geométrica (normalmente un rectángulo) y protegían tanto los flancos como la parte superior utilizando escudos. Los legionarios que ocupaban posiciones interiores cubrían la parte superior colocando el escudo sobre su cabeza, mientras que los que ocupaban los flancos llevaban dos y hasta tres escudos: uno para proteger la parte superior y uno o dos escudos (si estaban en la esquina) para proteger los laterales. Con esta formación, todos los legionarios quedaban protegidos por los escudos y eran muy difíciles de vencer.

Cuenta la historia que existió un general que estableció que la mejor figura para la formación no era la rectangular sino la cuadrada, de forma que el número de filas y columnas de legionarios coincidía. El problema al que se enfrentaba este general era decidir en cuántas formaciones (y de qué tamaño) debía separar su ejército para que:

  • No quedara ningún legionario fuera de una formación (aunque admitía formaciones de un único legionario).
  • Se minimizara el número de escudos necesarios para protegerlos.

Nuestro general, después de hacer muchos cálculos, decidió que la mejor manera de que estas dos condiciones se cumpliesen era comenzar haciendo el cuadrado más grande posible con sus legionarios. Con los que le quedasen libres volvía a repetir la operación, y así hasta que no quedasen legionarios que formar3.

Por ejemplo, si el número de legionarios en el ejército era 35, la manera utilizada por el general para hacer la formación consistía en un cuadrado de 25 legionarios (5×5), otro de 9 (3×3) y otro de 1 (1×1):

image-20221006175121262

1
2
3

assertEquals(ejercitoRomano.cuantosEscudos(35), 71);
assertEquals(ejercitoRomano.cuantosEscudos(20), 44);
assertEquals(ejercitoRomano.cuantosEscudos(10), 26);

Créditos

Autores: Marco Antonio Gómez Martín, Pedro Pablo Gómez Martín y Patricia Díaz García. Revisor: Catalina Molano Alvarado. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=119

¿Cuántas me llevo?

Cuando aprendemos a sumar números pronto nos cuentan aquello de “llevarse una”: cuando los dos dígitos que sumamos llegan a la decena tenemos “acarreo” que debemos sumar a los siguientes dígitos (de la izquierda).

Cuando nuestros maestros nos ponían ejercicios, antes tenían que contar cuántas veces tendríamos que “llevarnos una” y en base a eso medían la dificultad del ejercicio.

¿Puedes hacer un programa que automatice esa tarea?

1
2
3

assertEquals(cuantasMeLlevo.calcular(123, 456), 0);
assertEquals(cuantasMeLlevo.calcular(555, 555), 3);
assertEquals(cuantasMeLlevo.calcular(123, 594), 1);

Créditos

Autores: Marco Antonio Gómez Martín, Pedro Pablo Gómez Martín y Patricia Díaz García. Revisor: Catalina Molano Alvarado. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=124

Llenando piscinas

Se acerca el verano y llega el momento de sacar de los armarios y trasteros las piscinas para los niños (y no tan niños), colocarlas en la terraza, patio o jardín y llenarlas de agua para que los pequeños de la casa puedan empezar a disfrutarlas.

Este año la tarea se presenta complicada porque durante el invierno la larga manguera que permitía llevar el agua desde el grifo de la cocina hasta la propia piscina se ha perdido y habrá que hacerlo con un barreño…

Para complicar aún más las cosas, también durante el invierno la piscina (a pesar de ser de fibra de vidrio) se ha pinchado y pierde un poco de agua. Aún así, como los pequeños están ansiosos por darse un chapuzón decidimos llenarla cuanto antes, con pinchazo incluido, y luego mientras ellos disfrutan lo arreglaremos. Dado que la piscina está perdiendo agua constantemente, estará llena únicamente durante un instante de tiempo. En ese preciso momento dejaremos de hacer viajes a la cocina y nos pondremos rápidamente a arreglarla.

Como dice el refrán “mal de mucho consuelo de tontos”; la tarea de llenado será un poco más llevadera gracias al consuelo de saber que nuestro vecino está en la misma situación. A través del seto del jardín podemos verle haciendo viajes como un loco de su cocina a su piscina, para compensar el pinchazo que también él tiene. La pregunta es ¿quién tardará menos en llenar la piscina?

El método aceptará tres parámetros: Los tres primeros números indican los litros de agua de nuestra piscina (1≤ p ≤ 109), el número de litros de nuestro barreño (1 ≤ b ≤ 109) y por último los litros de agua que la piscina pierde durante el viaje. A continuación aparecen tres números para indicar la misma información pero de nuestro vecino.

Debe devolver 0 si empatan, -1 si gana el vecino y 1 en caso contrario

1
2
3

assertEquals(piscina.quienGana(10, 5, 1, 15, 6, 1), 0);
assertEquals(piscina.quienGana(50, 5, 1, 50, 5, 0), -1);
assertEquals(piscina.quienGana(50, 5, 1, 50, 5, 6), 1);

Créditos

Autores: Marco Antonio Gómez Martín, Patricia Díaz García y Pedro Pablo Gómez Martín. Revisor: Catalina Molano Alvarado. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=131

Escalera de color

La llamada baraja inglesa es una modificación menor de la baraja francesa. Sus similitudes son tan grandes, que es habitual considerarlas la misma. Contiene 52 cartas, distribuidas en 4 palos diferentes. Los palos se conocen con el nombre de picas (♠), diamantes (♦), tréboles (♣) y corazones (♥). De cada uno, hay trece cartas, con valores del 1 (al que se conoce como As) hasta el 10, más las tres figuras, Jack (J), Queen (Q) y King (K), que, numéricamente, serían los valores 11, 12 y 13. Las diferencias más notables entre la baraja francesa y la inglesa están en el nombre de la carta Jack (conocida en la francesa como Valet, V), y el As, nombre específico de la baraja inglesa que, además, desplaza su valor en muchos juegos del 1 al 14, convirtiéndola en una carta más poderosa que la K.

La baraja inglesa se utiliza en juegos mundialmente conocidos, como el bridge, la canasta o el póquer.

En este último, la jugada más valiosa es una escalera de color, que se forma cuando un mismo jugador consigue una mano de 5 cartas del mismo palo con valores consecutivos.

Cada carta se representa por su número contando J = 11, Q = 12, K = 13 y AS = 14

Al programa se le pasan 4 números de cartas y debe calcular la carta necesaria que habría que añadir a las cuatro recibidas para obtener la escalera de color más alta posible

1
2
3
4

assertEquals(escaleraDeColor.escalera(11, 12,13 ,14), 10);
assertEquals(escaleraDeColor.escalera(10, 12,13 ,14), 11);
assertEquals(escaleraDeColor.escalera(5, 6,7 ,8), 9);
assertEquals(escaleraDeColor.escalera(9, 12,13 ,14), 0);

Créditos Autores: Patricia Díaz García, Marco Antonio Gómez Martín y Pedro Pablo Gómez Martín. Revisor: Catalina Molano Alvarado. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=134

Números vampiro

En 1994, Clifford A. Pickover puso de manifiesto la existencia de los temidos números vampiro. Los números vampiro sobreviven ocultos entre el resto de nuestro sistema numérico, conservando los genes de sus padres tras multiplicarse. Así, por ejemplo, el número 2.187 es un número vampiro, al tener los mismos genes (dígitos) que sus dos progenitores, 27 y 81 (27 · 81 = 2.187).

Los números vampiro verdaderos (con pedigrí) cumplen cuatro condiciones:

  • Tienen un número par de dígitos.
  • Se obtienen al multiplicar dos números, llamados colmillos, que tienen la mitad de dígitos que el original.
  • Tienen los mismos dígitos que los colmillos, y en la misma cantidad (aunque en cualquier orden).

Como con los vampiros humanos, los números vampiro no son fáciles de detectar. ¿Puedes ayudarnos?

Para simplificar, en número debe estar comprendido entre 1000 y 9999

1
2
3
4
5
6
7
8

assertTrue("Error", vampiros.esVampiro(1260));
assertTrue("Error", vampiros.esVampiro(1395));
assertTrue("Error", vampiros.esVampiro(1435));
assertTrue("Error", vampiros.esVampiro(1530));
assertTrue("Error", vampiros.esVampiro(1827));
assertTrue("Error", vampiros.esVampiro(2187));
assertTrue("Error", vampiros.esVampiro(6880));
assertFalse("Error", vampiros.esVampiro(6881));

Créditos Autores: Pedro Pablo Gómez Martín, Marco Antonio Gómez Martín y Patricia Díaz García. Revisor: Catalina Molano Alvarado. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=125

Números cubifinitos

Se dice que un número es cubifinito cuando al elevar todos sus dígitos al cubo y sumarlos el resultado o bien es 1 o bien es un número cubifinito.

Por ejemplo, el número 1243 es cubifinito, pues al elevar todos sus dígitos al cubo obtenemos 100 que es cubifinito.

Por su parte, el 513 no es cubifinito, pues al elevar al cubo sus dígitos conseguimos el 153 que nunca podrá ser cubifinito, pues la suma de los cubos de sus dígitos vuelve a dar 153.

Dado un número, se trata de determinar si éste es o no cubifinito.

Usa un Set para almacenar los números ya calculados

1
2

 Set<Integer> set;
 set = new TreeSet<>();

1
2
3
4
5

assertTrue("Error", cubifinito.esCubifinito(1));
assertTrue("Error", cubifinito.esCubifinito(10));
assertTrue("Error", cubifinito.esCubifinito(1243));
assertTrue("Error", cubifinito.esCubifinito(87418));        
assertFalse("Error", cubifinito.esCubifinito(513));

Créditos Autor: Marco Antonio Gómez Martín. Revisor: Pedro Pablo Gómez Martín. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=139

Paréntesis

Se entiende que una secuencia de caracteres está correctamente equilibrada con respecto a los paréntesis si cada uno de los paréntesis de apertura tiene su paréntesis cerrado. Cuando añadimos otros mecanismos de agrupación (como los corchetes, [ y ] o las llaves, { y }), el equilibrio se da si el número de aperturas de cada símbolo coincide con el de cierres y además se cierran en el orden correcto.

Se trata de implementar un programa que indique si una cadena está correctamente balanceada con respecto a paréntesis, corchetes y llaves.

1
2

assertTrue("Error", parentesis.esBalancenado("[{[(hola)]}]"));
assertFalse("Error", parentesis.esBalancenado("{(hola)]}]"));

Créditos Autor: Marco Antonio Gómez Martín. Revisor: Pedro Pablo Gómez Martín. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=141

Año 2013

Mary lleva muchos años redactando cartas para sus jefes. Cuando comenzó el año 2013, observó con fastidio que al poner la fecha se veía obligada a utilizar más teclas diferentes que otras veces. Empezó a hacer memoria y se dio cuenta de que, tras 25 años, el año 2013 era el primero que tenía sus cuatro dígitos diferentes. Desde 1988, todos los años habían tenido al menos un dígito repetido.

La serie de años sin dígitos repetidos que comienza con 2013 terminará en 2019. En 2020 comenzó una serie nueva de números con dígitos repetidos, que se mantendrá hasta el 2030, incluido.

El método debe indicar el primer año de la serie de números con o sin dígitos repetidos a la que pertenece.

1
2
3

assertEquals(anyo2013.primeroSerie(1990), 1988);
assertEquals(anyo2013.primeroSerie(2015), 2013);
assertEquals(anyo2013.primeroSerie(2025), 2020);

Créditos Autores: Pedro Pablo Gómez Martín, Patricia Díaz García y Marco Antonio Gómez Martín. Revisores: Ferran Borrell Micola, Cristina Gómez Alonso, Catalina Molano Alvarado y Roger Meix Mañá. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=174

Expresiones aritméticas

Las expresiones aritméticas suelen escribirse utilizando lo que se conoce como notación infija en la que los operadores se colocan entre los operandos. Esta notación, intuitiva para los humanos, tiene el problema de obligarnos a poner paréntesis en ciertas ocasiones para cambiar el orden de aplicación de los operadores.

Por otro lado, la notación postfija consiste en colocar el operador tras los dos operandos; una de sus ventajas es que no necesita paréntesis. Además es fácilmente evaluable con una pila. El proceso de evaluación consiste en añadir a la pila los operandos que nos vayamos encontrando. Cuando leemos un operador, extraemos dos valores de la pila los combinamos con el operador encontrado (teniendo en cuenta que el primer valor que se extrae es el segundo operando de la operación) y añadimos el resultado de vuelta.

Existe otra posibilidad de notación que sigue la misma idea que la anterior pero en vez de utilizar una pila para la evaluación, utiliza una cola. Cuando se tienen que añadir elementos a la cola, se hace por detrás, mientras que la extracción se realiza por delante.

Dada una expresión, nos preguntamos si, al ser considerada escrita en cada una de las dos notaciones, dará el mismo resultado, uno distinto, o incluso si la expresión no será correcta en alguna de las dos (debido a división por cero).

Debes escribir dos métodos, uno para la pila y otro para la cola a los que se pasa una expresión. Cada elemento de la expresión debe estar separado por un espacio en blanco:

1
2
3
4
5
6
7
8

assertEquals(evaluarExpresion.pila("5 1 2 + 4 * + 3 -"), "14");
assertEquals(evaluarExpresion.pila("2 4 5 3 / * +"), "6");
assertEquals(evaluarExpresion.pila("6"), "6");
assertEquals(evaluarExpresion.pila("3 5 4 + *"), "27");

assertEquals(evaluarExpresion.pila("8 1 1 - /"), "ERROR");
assertEquals(evaluarExpresion.pila("1 1 - 8 /"), "0");
assertEquals(evaluarExpresion.pila("0 0 /"), "ERROR");

Créditos Autor: Marco Antonio Gómez Martín. Revisor: Pedro Pablo Gómez Martín. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=198

Números afortunados

Dado un N ≥ 2, se llaman números afortunados a los que resultan de ejecutar el siguiente proceso: se comienza generando una lista que contiene los números desde 1 hasta N en este orden; se elimina de la lista un número de cada 2 (es decir, los números 1, 3, 5, etc.); de la lista final resultante se elimina un número de cada 3, etc. El proceso termina cuando se va a eliminar un número de cada M y el número de elementos que quedan es menor que M. Los números que queden en la lista en este momento son los afortunados.

1
2
3
4

assertEquals("2", Afortunados.calcular(3).trim());
assertEquals("4 6 10", Afortunados.calcular(10).trim());
assertEquals("10 12 18 22 30", Afortunados.calcular(30).trim());
assertEquals("30 34 42 48 58 60 78 82", Afortunados.calcular(100).trim());

Orden

Dado un array de 10 números enteros, la aplicación debe indicarnos si los números están ordenados de forma creciente, decreciente, o si están desordenados

1
2
3
4
5
6
7
8

int [] numeros = {1,5,7,9};
assertEquals(Orden.comprobar(numeros) , 1);
int [] numeros2 = {9, 5, 4, 3};
assertEquals(Orden.comprobar(numeros2) , 2);
int [] numeros3 = {9, 5, 7, 3};
assertEquals(Orden.comprobar(numeros3) , 3);
int [] numeros4 = {9, 9, 9, 9};
assertEquals(Orden.comprobar(numeros4) , 0);

Persistencia multiplicativa

En 1973, el matemático inglés Neil Sloane definió, en una revista dedicada a las matemáticas recreativas, la persistencia multiplicativa de los números. Consiste en el número de veces que hay que multiplicar los dígitos de un número (escrito en base 10) hasta llegar a un número de un único dígito.

​ Por ejemplo, el número 39 tiene una persistencia multiplicativa de 3:

1

  39 -> 3*9 = 27 -> 2*7 = 14 -> 1*4 = 4

1
2
3

assertEquals(Persistencia.calcular(39), 3);
assertEquals(Persistencia.calcular(931), 3);
assertEquals(Persistencia.calcular(245), 2);

Autores: Pedro Pablo Gómez Martín, Marco Antonio Gómez Martín y Patricia Díaz García. Revisores: Ferran Borrell Micola, Cristina Gómez Alonso y Roger Meix Mañá.Ç Fuente: https://www.aceptaelreto.com/problem/statement.php?id=182

Ordenación por el método de la burbuja

Según la Wikipedia El ordenamiento de burbuja (Bubble Sort en inglés) es un sencillo algoritmo de ordenamiento. Funciona revisando cada elemento de la lista que va a ser ordenada con el siguiente, intercambiándolos de posición si están en el orden equivocado. Es necesario revisar varias veces toda la lista hasta que no se necesiten más intercambios, lo cual significa que la lista está ordenada. Este algoritmo obtiene su nombre de la forma con la que suben por la lista los elementos durante los intercambios, como si fueran pequeñas “burbujas”. También es conocido como el método del intercambio directo. Dado que solo usa comparaciones para operar elementos, se lo considera un algoritmo de comparación, siendo uno de los más sencillos de implementar.

Reversible

Se denomina número reversible a aquél que al ser sumado a sí mismo tras invertir sus dígitos da como resultado un número en el que todos los dígitos son impares.

Por ejemplo, el número 36 es reversible pues 36 + 63 = 99, y los dos dígitos de 99 son impares. Fíjate que esto significa que también el número 63 es reversible. También lo son el 409 y el 904.

Para ser considerado número reversible, la cantidad de dígitos del número y de su versión invertida debe ser el mismo. Por tanto, el número 1010 no es reversible, incluso aunque 1010 + 0101 = 1111. No se considera válido porque 0101 es en realidad el número 101, que tiene menos dígitos que 1010.

1
2
3

assertTrue("ERROR", Reversible.esReversible(63));
assertTrue("ERROR", Reversible.esReversible(43));
assertFalse("ERROR", Reversible.esReversible(1010));

Créditos Autores: Pedro Pablo Gómez Martín, Marco Antonio Gómez Martín y Patricia Díaz García. Revisores: Ferran Borrell Micola y Cristina Gómez Alonso. Fuente: https://www.aceptaelreto.com/problem/statement.php?id=193

Números de Lychrel

Cuando se aburren, los aficionados a las matemáticas se dedican a jugar con los números. Eso les lleva, por ejemplo, a coger cualquier número, darle la vuelta y sumarlo a sí mismo, repitiendo el proceso una y otra vez hasta dar con un número capicúa. Por ejemplo, para el 91 llegamos a un capicúa en sólo dos pasos:

1
2

91 + 19 = 110
110 + 011 = 121

Algunos números se resisten a alcanzar un capicúa. El 196 es el número más pequeño para el que no se ha llegado a ninguno, por más que se ha intentado. Los matemáticos no han podido demostrar que, efectivamente, no vaya a llegarse a uno. Mientras continúan buscando una demostración, los aficionados siguen sumando y sumando con la esperanza de llegar a él. Los números con los que, se sospecha, no puede alcanzarse un capicúa se conocen como números de Lychrel. Curiosamente, algunos números capicúa parecen ser también números de Lychrel.

Se pide calcular en cuántas iteraciones hay que dar para llegar a un número capicúa. El programa debe devolver -1 si se llega en el proceso a alcanzar el número 1.000.000.000.

1
2
3
4

assertEquals(2,Lychrel.iteraciones(91));
assertEquals(-1,Lychrel.iteraciones(196));
assertEquals(-1,Lychrel.iteraciones(4994));
assertEquals(4,Lychrel.iteraciones(5445));

Créditos Autores: Pedro Pablo Gómez Martín, Marco Antonio Gómez Martín y Patricia Díaz García.

Fuente: https://www.aceptaelreto.com/problem/statement.php?id=205